In this article, you're presented with shapes and platonic solids as they relate to F#. How do geometric shapes relate to creation? Do they play a part in the recipe of creation? What are we to do with this information?
These are the types of questions we explore during any research and discovery process. I don't have the answers but what I do have is the information. What readers do with that information is up to you. Why do I even present it here? When I find patterns that appear to fit within a larger puzzle, it's time to pay attention. The entire Frequencies of Creation series is about the note, F#. We see it everywhere in creation. Why is that? At this point, I can only speculate. I suspect that once a few scientists weigh in on the topic, more puzzle pieces will come together and we'll have a bigger picture. If you're a scientist, cosmologist, or mathematician, I'd love to hear from you for your perspective on this topic!
NOTE: There is no complimentary video for this post since everything we're looking at is visual.
Here's what we know so far...
Exploring "all things F#"
Before we go into the meat of this post concerning the platonic solids and other geometric shapes, let's first gather information about the F# harmonic series and the F# Major scale. This is needed so you can compare that information with everything related to the key of F# Major.
Remember... we can build a harmonic series (also known as the overtone series) from ANY note as the fundamental (main note) frequency. That main note is heard by the ear with "colors and spices" of additional higher notes. The strength/weakness of the sympathetic vibrations of those additional notes tells our ears what instrument or voice we're hearing. Any note without harmonics is called a "sine wave."
Literally, the harmonics present in every voice or instrument is a "voice print." This is true with sounds we consider non-musical as well. Most of us recognize the difference between a chainsaw and a car engine. Why is that? There are different harmonics present in the two types of engines. Our ears have memorized what each engine sounds like. In addition, we recognize people by their voices without having to see them because we've learned the sound (timbre) of the voices.
First, we'll look at the F# harmonic series...
We'll start with the third F# from the bottom end the piano (F#2 or 4th line F# in the bass clef). NOTE: Since every note has its own harmonic series, all partials and specific Hz frequencies adjust for that note. I've chosen the F# just below middle C on the piano that resonates at 180 Hz in the A=432 concert pitch because it represents the first geometric shape (a triangle).
This is the harmonic series for the 4th line F# in the bass clef:
- Partial 1: 4th line F# in the bass clef (180 Hz)
- Partial 2: 1st space F# in the treble clef (360 Hz)
- Partial 3: 3rd space C# in the treble clef (540 Hz)
- Partial 4: 5th line F# in the treble clef (720 Hz)
- Partial 5: Ledger line A# in the treble clef (900 Hz)
- Partial 6: Ledger line C# in the treble clef (1080 Hz)
- Partial 7: Ledger line E in the treble clef (1260 Hz)
- Partial 8: Ledger line F# in the treble clef (1440 Hz)
- Partial 9: Ledger line G# in the treble clef (1620 Hz)
- Partial 10: Ledger line A# in the treble clef (1800 Hz)
- Partial 11: Ledger line C in the treble clef (1980 Hz)
- Partial 12: Ledger line C# in the treble clef (2160 Hz)
- continue on until infinity
Here is the sheet music version of the F# harmonic series. Take notice of which notes from this harmonic series are also found in other places.
KEY:
The numbers above each note indicate the partial.
Hz frequencies are listed below each note.
The notes in red indicate they are an octave higher than written.

Now, look at the notes within the F# Major scale...

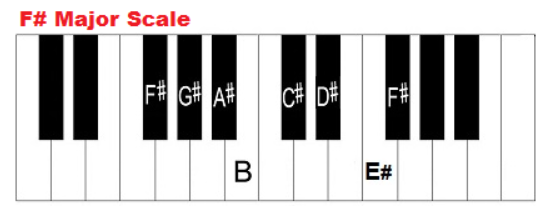
Compare the F# harmonic series with the F# Major scale (above). It may help to become familiar with what notes are in the F# Major scale as we continue this series. REMEMBER: Although E# is another name for F, we call it E# because there's already an F note represented in the F# scale. In music, we get to "spell" key signatures based on context just like in English, we spell same-sounding words differently based on their context (to, two, and too as an example).
Notice that as the harmonics get higher, the notes are closer together. Because the fundamental frequency is F#, many partials (1, 2, 4, and 8) are F#. This adds strength to the sound of the F# note. Since octaves, Perfect 5ths, and Perfect 4ths are the most prominent "sympathetic" notes heard in any given note's overtones, you'll see them more frequently within the various partials of any given harmonic series.
Partials 4, 5, and 6 spell an F# Major triad (F# - A# - C#). We see right up front that Major chords are strongly present in every fundamental note. Partials 8, 10, and 12 spell another F# Major triad. Because the note, A (creating f# minor), doesn't show up until the 19th harmonic, the strength of minor chords is much weaker. However, that A will show up in "sister" notes and keys related to F# Major earlier on in that notes harmonic series. But, that's music major stuff hardly anyone but music theory geeks care about so we'll leave it alone here.
Some key points to remember: 1) the lower the partial, the more present that "sympathetic" sound is heard within a given note. 2) As the partials go higher, so do the pitches. 3) As the partials go higher, the notes are closer together. 4) The harmonic series goes until infinity.
Looking at geometric shapes
In my process of researching, I recognized that numbers are important. Think about it... everything about computers is based on 0's and 1's. Two simple numbers control everything you're reading in this post. Hebrew gematria (numerology) is a numbering system for each letter of the Hebrew alphabet. Most ancient languages followed the Jews in this protocol. For most pre-twentieth-century societies, numerology was a huge deal! Numerology IS the study of math as it relates to subjects outside mathematics.
Math can explain everything in the universe. When I see numbers, I wonder, "If I turn a number into a frequency, what note would it be?" Curiosity got the better of me, which is partially what leads me to many of my discoveries. This question led to the reason I kept seeing notes within the F# scale that are present in the strangest of places. As I state in Part 1 of this series, when there are patterns, go down that rabbit hole! See what's there and collect information to analyze later.
Now... onto numbers in geometric shapes as they're compared to F#
Scroll back up and look at the Hz numbers for the F# harmonic series. Take note of the numbers 180, 360, 540, 720, 900, 1080, 1260, 1440, and 1620. We'll, we're about to see them somewhere besides a musical frequency...
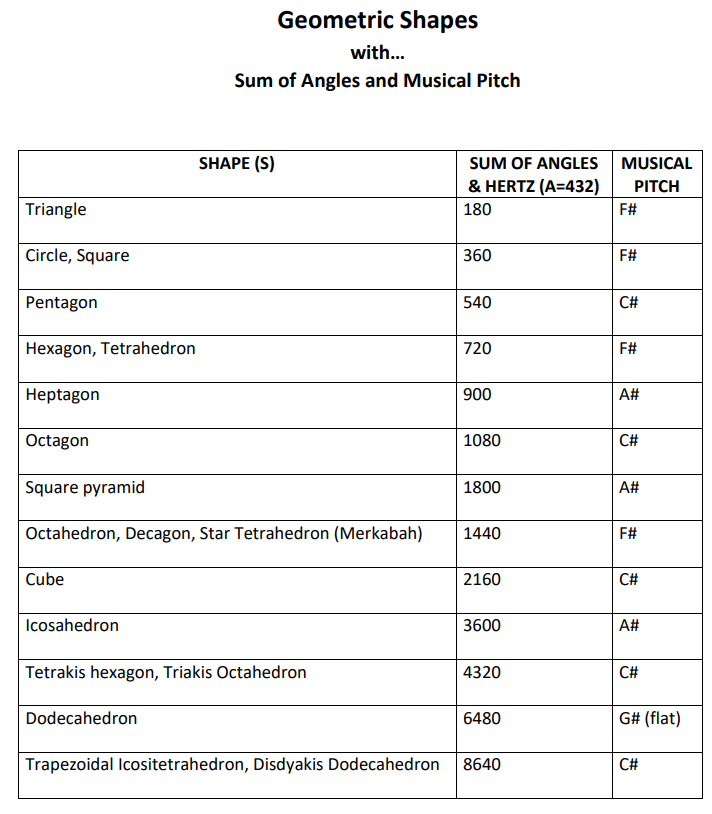
The five platonic solids are: Tetrahedron, Octahedron, Cube, Icosahedron, Dodecahedron.
As indicated in the picture, the numbers represent the SUM of all the angles for each shape. Notice the order they all appear, fitting quite nicely within the F# harmonic series. It's a very close match, with the exception of a few notes. You'll see all notes represented by a shape are part of an F# Major triad or scale. And, the first five partials exactly match the first five shapes. After that point, notes not directly associated with the F# Major scale aren't represented by a geometric shape.
- Partial 1: F# in the bass clef (180 Hz) triangle
- Partial 2: F# in the treble clef (360 Hz) circle, square
- Partial 3: C# in the treble clef (540 Hz) Pentagon
- Partial 4: F# in the treble clef (720 Hz) Hexagon, Tetrahedron
- Partial 5: A# in the treble clef (900 Hz) Heptagon
- Partial 6: C# in the treble clef (1080 Hz) Octagon
- Partial 7: E in the treble clef (1260 Hz) this one is skipped but is part of an f# minor scale.
- Partial 8: F# in the treble clef (1440 Hz) Octahedron
- Partial 9: G# in the treble clef (1620 Hz) this one is skipped but is part of the F# Major scale
- Partial 10: A# in the treble clef (1800 Hz) Square pyramid
- Partial 11: C in the treble clef (1980 Hz) this one is skipped and is not part of either an F# Major or f# minor scale/triad.
- Partial 12: C# in the treble clef (2160 Hz) Cube
What does this mean?
I don't have the answer to this question. I suspect there are connections that I'm not yet aware of. What I do know is that the F# Major triad plays a very important part in geometric shapes. The shapes are a prominent feature in sacred geometry, which I've not studied enough at this point to comment on. I do know that numbers, when converted to frequencies for geometric shapes, seem to align with what's in our DNA. What are the odds of that? Remember that the two most prominent notes in our DNA are F# and C#? For a refresher on that information, read Part 3 of this series.
The similarities between all the F#'s in nature, the cosmos, and our body, appear to be more than chance. How it's all connected, we'll continue to explore in future posts of this series.
Del Hungerford, November 2022
NOTE: None of the information in this series or any other article on this site may be used without permission! You may share the articles but if you wish to quote my work in your own writing, it is "good form" to cite any materials that aren't your own.

