The final post in the frequencies of creation series is fitting for the periodic table, especially since one of the most important features of the "universal weave" is the number 7. We start at the beginning of time when the universe was void and without form...
Russell A. Smith (R. Smith hereafter) found the “universal weave” based on teachings of a man named George Gurdjieff and didn’t connect it with the periodic table until he saw that the family groups in his diagram perfectly matched the four families of the periodic table. He called his work the “law of threes” and the “law of sevens.” He connected ratios in music to the universal laws, which ancients had done for quite some time. The law of three requires that THREE notes determine chord quality (major, minor, augmented, diminished). There are seven notes in major, minor, and modal scales. Eastern scales and some additional western scales (pentatonic, whole tone, etc.) have varying numbers of notes within each scale.
The basics of how R. Smith's method works is to start from 1296 Hz and create a descending scale using the ratios provided in his chart. But he did it much like a piano tuner and began at a certain point, jumping from interval to interval according to specific ratios that filled in the notes for each scale. Because each minor 3rd interval (m3) is pure according to the ratios Russell used, this creates slight differences in pitches from scale to scale so the m3 remains close to pure across the board.If we go back to the beginning where cosmologist Mark Whittle (link below) describes the sound that came from what many call the “big bang,” we have a better picture of the creation process. Whatever definition people want to use, it’s obvious something was a catalyst for the universe we know today. That sound was an F# where the first harmonic that came out of the original sound was the minor 3rd (m3), the note A. From there, the m3 changed into a Major third (M3), going up a ½ step to the note A#.
In looking at how the periodic table came to be, everything starts with a m3 (E – C#) 1s Hydrogen and 1s Helium. From there, after a change in concert pitch from A=432 to A=450 as 2s Beryllium moves across the table to the 2p subshell (Boron – Neon), what should be a M3 becomes an augmented 4th or diminished 5th – creating the dreaded (and most dissonant note) the “tri-tone.” That tri-tone must be resolved. That occurs for the A in the 3s series for (Sodium and Magnesium)! The tri-tone resolves inward, creating the first Perfect 4th in the periodic table.
NOTE: Even if another starting pitch other than 1296 Hz with different notes were to be used, the intervals remain the same because R. Smith's periodic table pitches are based on ratios, not specific musical notes.
The first 2 elements (hydrogen and helium) existed by themselves for quite some time. The next 8 elements (up through neon) completed the first round through the process of nuclear fission. Scientists say the remaining elements came from supernova explosions. As we continue this musical journey through the periodic table, there should be other indicators of when and how that occurred through looking at the musical intervals.
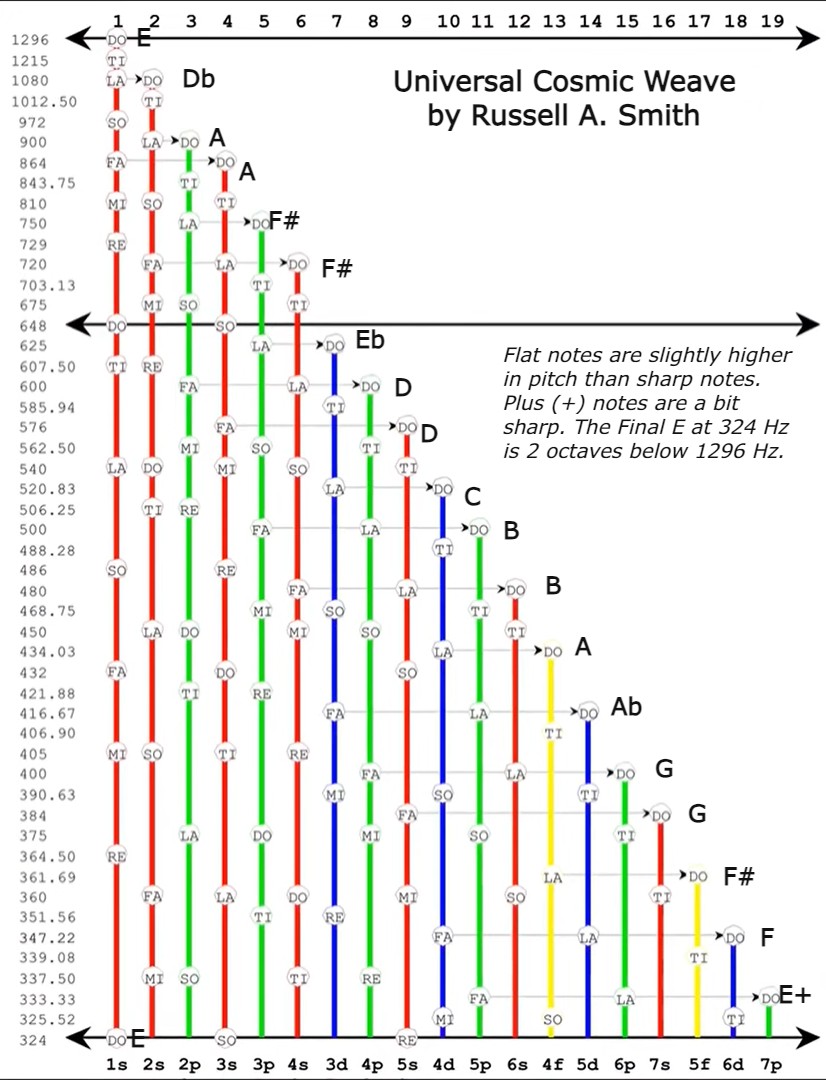
Figure 1
In Figure 1, Hz frequencies are listed on the left. Those frequencies were used to find the pitch for each DO. The “family” groups are listed across the bottom (1s, 2s, 2p, 3s, etc.). The musical keys are listed next to their proper DO. Each vertical column represents a major scale in the key of each DO. Specific Hz varies so intervals remain pure. The concert pitch toggles back and forth between A=430, A=432, A=434, and then back to A=432. In Figure 2, the frequencies are listed in the order they appeared with the atom at the center and each required subshell expanding from there.
NOTE: The images in Figure 1 and Figure 2 are screenshots from the R. Smith's YouTube video (link at the end). I revised the images by adding the specific musical notes and additional labels to his charts.
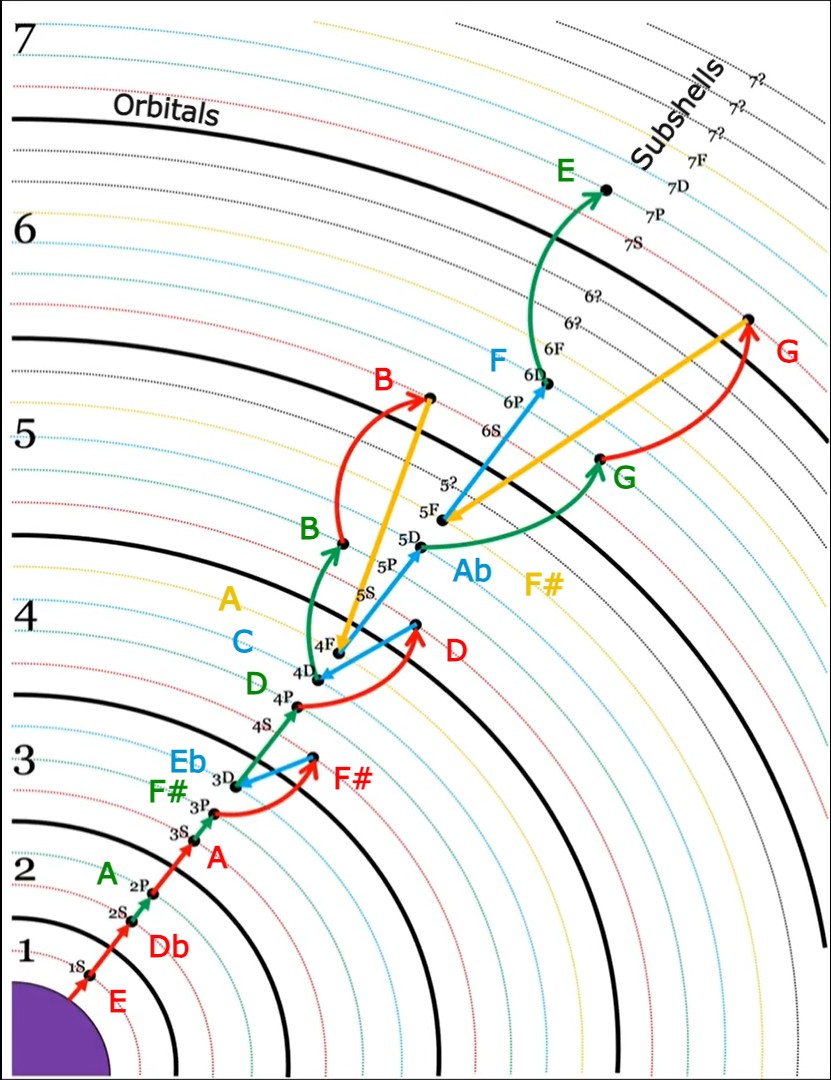
Figure 2
From the original DO for the 1s (key signature of E at 1296 Hz), there’s a descent of a m3 to the LA of the key of E (the note C#/Db). The C# then becomes the new DO (Db for 2s) where it continues a downward ascent to fit the FA, LA, DO pattern as described by Russell. As the descent of notes weaves from key to key through the family tree, the pitch needs adjusting to keep the intervals “pure.” The fractions Russell used to come up with the frequencies are the same for each interval. However, this requires a slight adjustment in Hz frequencies. This is why there are several additional Hz numbers for the same note name. Depending on the starting note, the 2nd note of the interval needs to adjust to the first interval so it’s in tune. Although several Hz frequencies are listed, many function as “passing tones” to get from one key to the next so everything is in perfect harmony.
Figure 3 shows the subshells in order or movement using the colors that R. Smith assigned them. It basically takes what's in Figure 2 and shows how the subshells move from one family group to the next horizontally. Each subshell starts with the Supreme (s) family group.

Figure 3
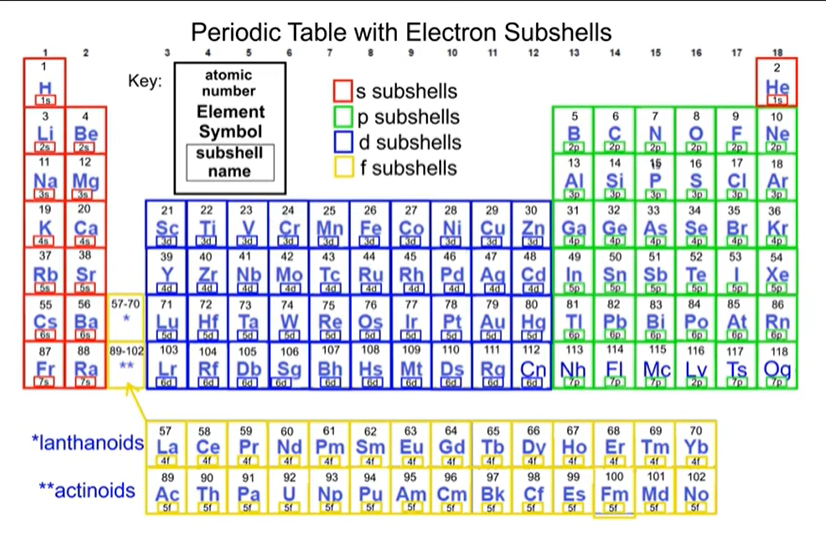
The entire Supreme family takes up the left two columns of the periodic table that begins each row (1s, 2s, 3s, etc.). The Supreme’s are the seven “parents” that indicate a new beginning for each row (period) of the table. The final column of every row ends with a “big ending” – an unreactive noble gas because all the electron subshells of that element are filled. The element before a noble gas is called a “halogen” when it’s in the Prime (p) subshell. It’s very reactive because it needs one electron to complete outer subshells. See R. Smith's version of the periodic table in Figure 7.
- Subshells fill in outer orbitals in order of creation.
- Dualities (orbitals of subshells) typically fill in one electron at a time in each successive duality. Duality is an elements orbital. It will either be a major oscillation (like hydrogen) or minor (like Helium): a = major and b = minor.
- The creation of Hydrogen and Helium was an ascending octave occurring in time, but followed the pattern that was already laid down in potenia as physical law – the cosmic weave of the 19 outer octaves.
- Major (+) oscillations receive electrons first starting with the duality closest to 1s before other dualities receive their second minor (-) oscillation electrons. Sometimes, major oscillations in outer subshell will borrow an electron or two from the minor oscillations of the outer most orbitals of the next earlier subshell.
Musical Comparisons
Figures 1, 2, and 3 all show the same thing but in a different manner. Figure 1 shows the starting frequency of 1296 Hz (E in the A=432 concert pitch). Descend to LA (a m3 lower at 1080 Hz) in the key of E to C#. C# becomes the new DO but since it’s enharmonic with Db, C# is renamed Db. This is also the case with A# and Bb (same note but two names). The key of C# is rarely used so it’s called Db. The same is true with A#/Bb. There is no key of A# so it’s called Bb. The keys of Gb and F# are both used.
From the original E, the descent continues until the final 324 Hz (E) is reached, which is 2 octaves lower than the original E at 1296 Hz. The E at 325.52 Hz (MI in 4d) needs an adjustment for the Pythagorean comma that resolves to the RE – SO – DO sequence (pitch of 324 Hz) in 1s, two octaves lower than the 1296 Hz DO that began the two-octave descent. RE – SO – DO can be visualized as a cadence in the key of E. RE (f# minor chord) is a ii chord in root position. Keep the F# as lowest note of the chord for SO (B Major chord) making it a V chord in second inversion that finally resolves to E Major. E is the pedal note that’s consistent (and works) with this simple ending ii – V6 – I chord progression, which is a popular chord progression in a lot of music.
R. Smith's chart shows the fractions that were used to determine musical frequencies from the original 1296 Hz. Everything begins from 1s and descends downward to achieve the next pitches within the various family groups until the final number 19 with the family “sub-section,” 7p. There are four “family” groups (electron subshells) within the family tree of the periodic table for a total of 19 rows of seven orbitals (dualities):
s (Supreme Family), p (Prime Family), d (Distant Family), and f (Final Family)

Figure 4
Musical keys are represented in each of the four families of the periodic table family tree. They are listed in the order they appear, which lines up with the 19 “octaves” R. Smith refers to. NOTE: There is a representation of TWO octaves musically, not 19 when looking at the Hz frequencies. For musical purposes, we’ll exchange “octave” for “tonic” because the tonic indicates the key signature. For example, in the key of E, the tonic is E. R. Smith mentions that the Supreme family is a “new beginning.” A new beginning is synonymous with a new key signature which begins with DO – the tonic note. DO is always the first note of a scale (when using movable, not fixed DO). If you choose to watch the video (link below), replace “octave” with “tonic” to understand it musically.
The periodic table family tree can be seen as follows: Great-grandparents or the first generation = Supreme. Grandparents or the second generation = Prime. Parents or the third generation = Distant. Great grandchildren or the fourth generation = Final. Within each family are cousins, aunts, uncles, etc. Musically, each represents a natural progression from one generation to the next. Here’s the musical keys (all major) that correspond to the various family “members” of the seven subshells.In Figure 5, I've added in the musical pitches for each of the four family groups along with their subshells and musical intervals. The graph is shown as follows:
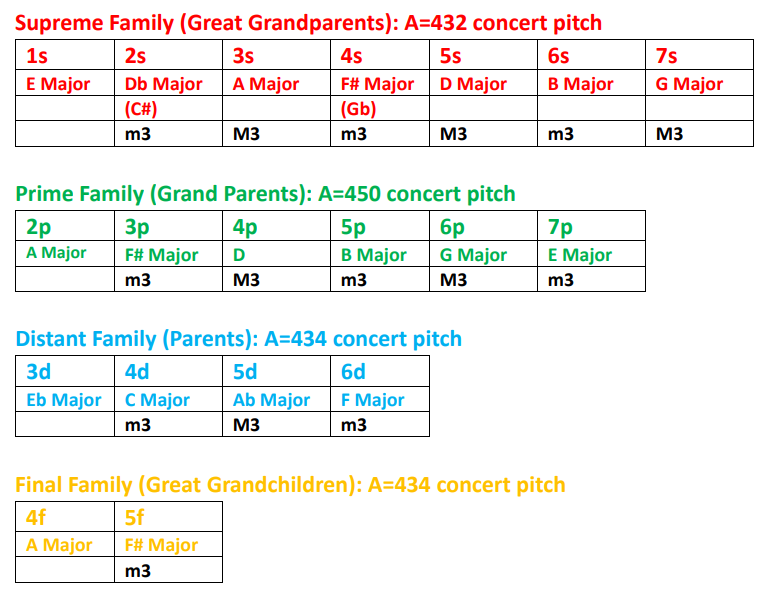
Figure 5
In Figure 6 is a new graph with a vertical representation of the subshells and their musical keys. R. Smith points out that everything is based on FA, LA, DO, which is made up of 3rd’s – both major (M3) and minor (m3). The temperament requires tuning each third by ratios (Pythagorean tuning) which is one reason the concert pitches meander. Eventually, the descending thirds take the whole sequence back to the beginning – from 1296 Hz to 324 Hz – both E’s but in different octaves within the A=432 concert pitch.
Thirds are the most difficult interval to play in tune. They must be “tempered” to be completely in tune (pure). This is the case for every key signature. Therefore, when moving from key to key by the interval of a third, the only way to make it work is to adjust the concert pitch for the M3. Pythagorean ratios fit within natural laws but when moving from key to key, it requires the temperament to adjust for the key changes within the periodic table. To be sure I was correct in my research, I put all the frequencies into a tone generator to check the intervals.
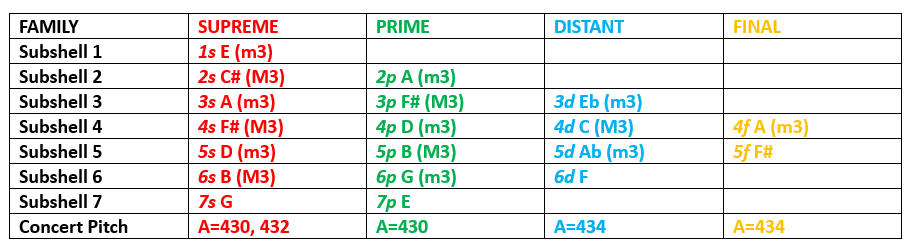
Figure 6
As mentioned earlier, R. Smith gets the starting pitch of 1296 Hz when beginning with 1 Hz (C) and figuring all other notes from there using Pythagorean ratios. He could have used any other starting note within the A=432 concert pitch. Simply follow the same mathematical formula he set out in his book and you'll have the new pitches. The other method of doing that if you're not a math whiz but are a music whiz is to transpose each note from the above chart up or down by the desired interval. For example, I could start with F# instead of E. That's a full step so all other notes would also go up 1 full step. The Supreme family's notes would then be (starting from the top) F#, D#, B, G#, E, C#, and A. Repeat the process for the other families.
To compare my charts with those put out by the YouTuber THEDOG Teachings (link below), I've included a screenshot from the video of the periodic table using his colors (Figure 7). CLICK HERE to see what else he has to offer.
Conclusion
The key here (no pun intended) is that musical intervals were part of the creative process for the universe. We see that in the periodic table. Without the elements, we wouldn’t have a universe and mankind would still be a thought. There are frequencies for creative purposes and specific pitches for other purposes. This introduction to the musical frequencies of the periodic table demonstrates that intervals play a major role in a creative process. We see this through the YHVH (m3) in the Tetragrammaton and when adding “the Christ” into the center of the name as the Shin (YHSVH), that adds the M3.
In the beginning was a note... out of that note came the m3 which then morphed into the M3. The "sound" was the voice of the Divine Creator who shows himself as YHVH (the m3). It goes from there and somehow fits within the periodic table. This will continue to be worked out as I continue to do more research.
Everything within music fulfills the law of threes and sevens. In music, it requires three notes for chord quality (major, minor, augmented, and diminished). There are seven notes in a musical scale with the 8th note being the octave of the “new beginning” (1st note) or “tonic” note. Just like there are seven subshells in the periodic table, there are seven notes in a musical scale.
Russell A. Smith is the first person I’ve seen that has a plausible explanation as to what the musical frequencies of the periodic table are. Even saying that, I believe it’s more about musical intervals than it is specific frequencies. In some creative instances, specific frequencies AND intervals may be used to work together. In addition, what R. Smith has discovered fits within natural laws (Pythagorean ratios) and matches what cosmologists have seen “at the beginning.” Not only that, but everything comes back to where it started, which matches Hebrew thought that everything is circular.
NOTE: This original post was created in late 2023. In May of 2024, many people sent me a video of Joe Rogan interviewing Terrance Howard. It was a fascinating interview where they spoke about the periodic table in the first part of the three-hour interview. Howard brought up some musical ideas that need adjusting so they fit within the natural laws of music. His research was based on the teachings of Walter Russell.
The one thing I've learned through this process is to pay attention to patterns! I didn't see a pattern that worked with the natural laws of music in Walter Russell's work. I had to do some digging... If a pattern can't be found, then try something else! R. Smith's version of the periodic table makes more sense because there is a repeatable pattern that works with the natural laws of music. His work was based on Gurdjieff's writings. Gurdjieff was a composer and understood music. Walter Russell wasn't a trained musician and his use of the term "octave" really means "cycle." The rest of Walter Russell's "musical" work on the periodic table could then be explained (possibly). I haven't done that part yet.
THE MAIN POINT...
- Look for patterns first and foremost.
- Make sure those patterns line up with natural laws.
- Bonus points if those patterns line up with other things in nature or other disciplines. As seen in this article, my findings line up with several scientists (archeaoacoustics, cosmologists, Hebrew gematria, crop circle measurements, ancient site acoustics, etc.). That's what you're looking for.
Until the next series... enjoy doing some scientific investigations on your own. Continue to send me cool videos, websites, and links.
Del
November 2023 with additions in May of 2024.
SOURCES:
Frequency Basics Course
If you're interested in learning more about how the universe works, purchase the 30 lessons in the Frequency Basics course ($150). There are nearly 300 pages of materials that cover a variety of frequency topics. The Frequencies of Creation series is included as part of that course with additional information.

