Overtones and A=432

The musical harmonic (overtone) series “partial” numbers when turned into Hertz, become the actual note names for the series. Confused? Let me explain…

What IS the harmonic series?

The harmonic series, or as musicians learn – “overtone series,” is the sequence of sounds where the main frequency (note) is heard the strongest. Additional higher notes are not as obvious but are part of each instrument’s sound. This is how we learn to identify the difference between a clarinet and a trumpet. Each instrument produces variations of the above overtones, making it similar to a DNA code – every instrument having its own unique “code.”

On this chart, the main note is shown as a low “C” in the bass clef. Within that “C” note are all the other notes above it that sound at a weaker volume level. What people recognize immediately is the lowest note even though the other notes are present in the overall sound of each note.

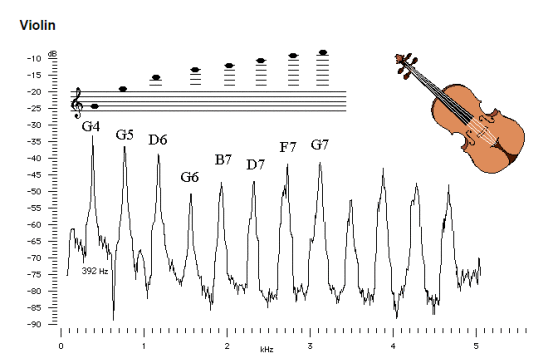As stated above, every instrument has their own unique combination of strong and weak overtones that specifically identify that instrument. Look at the violin overtones for the note “G” above middle “C.” You’ll see how the higher notes on the staff are also heard in the “G” note. If you put that note on a graph, this is what it would look like. There will be variations depending on how any given note starts and ends (attack and release). This graph shows the what I call ” violin DNA” or resonating harmonics specific to the violin. The graph will look basically the same for every note with minor differences in attack and release. changes.

 

Turning the numbers into pitches…

In the chart below: Column 1 represents the partial number. Column two lists the notes from the overtone series shown on the first chart in this post (above). In the third column, I took the partial number and wanted to see what actual Hertz those numbers might represent. I made a full A=432 chart starting from the number 1 and transferred those results to chart below. In the fourth column, I’ve taken the high/low pitch information from the first chart in this post and transferred it here. The fifth column represents the distance between one note to the next.

• PU = perfect unison
• P4 = perfect fourth
• P5 = perfect 5th
• M2 = major second (a whole step)
• m2 = minor second (a half step)
• m3 = minor third

The last column (to be discussed at a later time) is the numerical gematria for Hebrew. There is a connection but you’ll have to wait for that article.

 

 

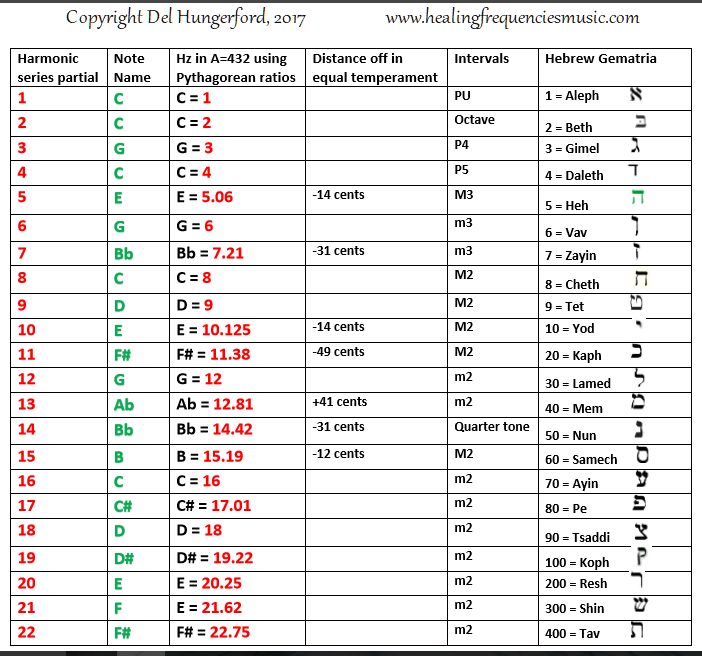
Look at the chart that I put together for the A=432 pitches/frequencies/Hertz. Compare/contrast those numbers with the first column in the above chart. You’ll notice for the partials where there’s a difference in the Hertz between columns one and three, the fourth column shows how it’s either sharp or flat. I didn’t continue on with partials 19 – 21 because that would require math, which isn’t one of my favorite things. If anyone would like to provide that information for me, I’ll add it to the chart.

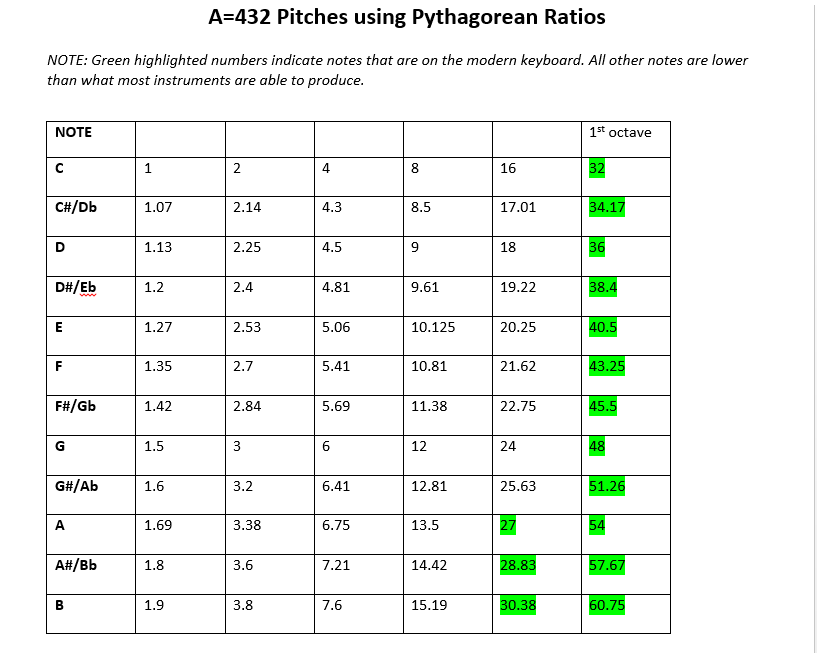
Conclusion

I won’t say a lot here but will point out the obvious… Don’t you find it interesting that when turning the number for the partial into a frequency, it becomes the exact same note (if you’re starting on “C”) as the partial itself? If you haven’t noticed that, look again. Partial 1 when given a Hertz is a very, very, low “C.” Partial 2 is also a “C” but an octave higher. Partial 3 when put as a Hertz, is a “G” and so on.

Isn’t it interesting that when you take the A=432 concert pitch and compare the partials of the note “C”to the harmonic series there’s a near perfect match? What are the odds of that? Feel free to comment below and while you’re at it, here’s an entertaining video about the harmonic series. Enjoy!

 

Del

© 2016 Del Hungerford

 

 

 

[mailerlite_form form_id=2]